【導讀】MEMS加速度計終于達到了能夠測量廣泛機器平臺振動的階段。其最近的能力進步,加上MEMS加速度計已有的相對于傳統(tǒng)振動傳感器的諸多優(yōu)勢(尺寸、重量、成本、抗沖擊性、易用性),促使一類新興的狀態(tài)監(jiān)控(CBM)系統(tǒng)開始使用MEMS加速度計。
結果,許多CBM系統(tǒng)架構師、開發(fā)者甚至其客戶首次考慮使用此類傳感器。他們面臨的問題常常是如何快速了解評估MEMS加速度計功能的方法,以便在其機器平臺上測量最重要的振動特性。這初看起來似乎很困難,因為MEMS加速度計數(shù)據(jù)手冊表述最重要性能特性的方式常常不是開發(fā)人員所熟悉的。例如,許多人熟悉用線速度(mm/s)來量化振動,但大多數(shù)MEMS加速度計數(shù)據(jù)手冊是用基于重力的加速度(g)來表達其性能指標。幸運的是,有一些簡單的技術可用來將加速度轉換為速度,以及估計加速度計關鍵特性(頻率響應、測量范圍、噪聲密度)對重要系統(tǒng)級標準(帶寬、平坦度、峰值振動、分辨率)的影響。
基本振動特性
先從慣性運動角度考察線性振動。在此背景下,振動是平均位移為零的機械振蕩。對于那些不希望其機器穿越整個車間的人來說,零平均位移非常重要!振動檢測節(jié)點中核心傳感器的價值與它反映機器振動最重要特性的能力高低直接相關。要評估特定MEMS加速度計在這方面的能力,首先必須從慣性運動角度對振動有一個基本了解。圖1是振動情況的物理示意圖,灰色部分表示中點,藍色部分表示一個方向的峰值位移,紅色部分表示另一方向的峰值位移。等式1提供了一個描述矩形物體瞬時加速度的數(shù)學模型,其振動頻率為(fV),幅度為Arms。
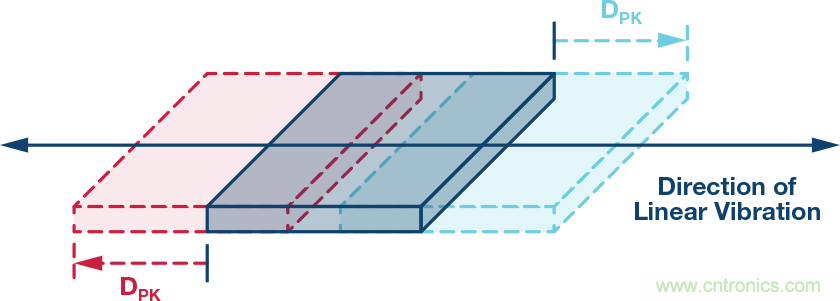
圖1.簡單線性振動
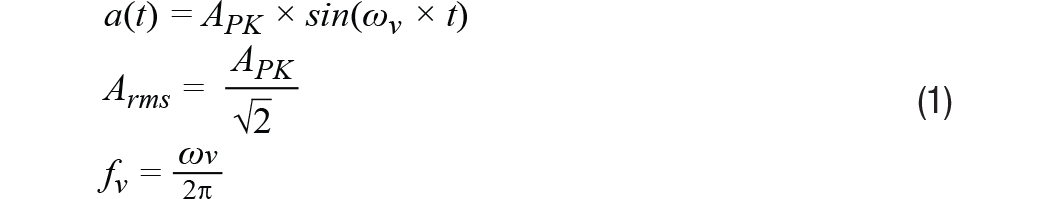
在大部分CBM應用中,機器平臺的振動常常有比等式1所示模型更復雜的頻譜特征,但此模型為學習發(fā)現(xiàn)之旅提供了一個很好的出發(fā)點,因為它給出了CBM系統(tǒng)常常會跟蹤的兩個常見振動特性:幅度和頻率。此方法對關鍵特性到線性速度項的轉換也很有用(稍后將有更多說明)。圖2提供了兩類不同振動模式的頻譜視圖。第一類(參見圖2中的藍線)在其頻率范圍(f1到f6)內具有恒定幅度。第二類(參見圖2中的紅線)在四個不同頻率處出現(xiàn)了峰值幅度:f2, f3, f4, 和 f5.
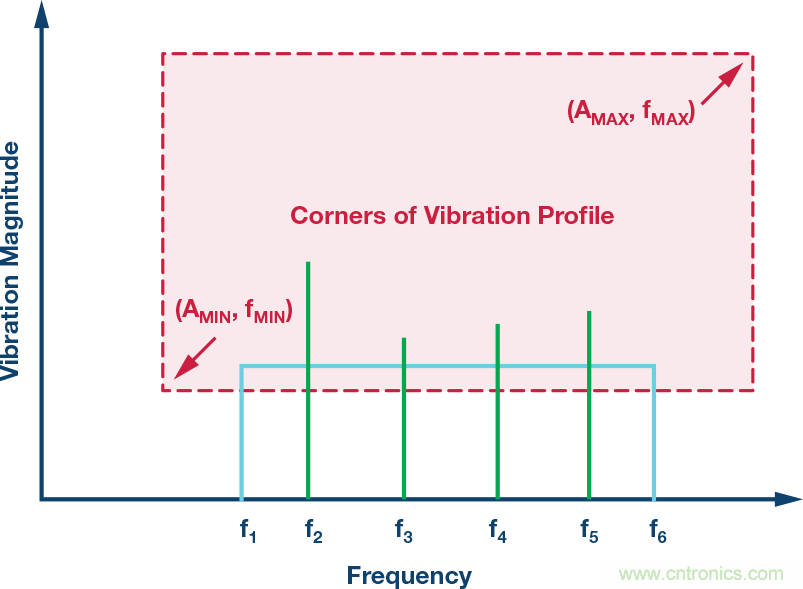
圖2.CM振動模式示例
系統(tǒng)要求
測量范圍、頻率范圍(帶寬)和分辨率是用來量化振動檢測節(jié)點能力的三個常見特性。圖2通過虛線矩形框顯示了這些特性,其邊界分別對應最低頻率(fMIN)、最高頻率(fMAX)、最小幅度(AMIN)和最大幅度(AMAX)。當考慮將MEMS加速度計用作振動檢測節(jié)點中的核心傳感器時,系統(tǒng)架構師很可能想在設計早期分析其頻率響應、測量范圍和噪聲行為。有一些簡單的技術可用來評估加速度計的各種特性,進而預判其是否滿足指定的一組要求。很顯然,系統(tǒng)架構師最終必須通過實際驗證和鑒定來核驗上述估計,但由對加速度計能力的早期分析和預測所得來的期望對這些工作是有價值的。
頻率響應
圖2提供了一個簡單的一階模型,其描述了時域中MEMS加速度計對線性加速度(a)的響應(y)。在該關系中,偏置(b)表示傳感器無振動時的輸出值。比例因子(KA)表示MEMS加速度計響應(y)相對于線性加速度(a)變化的改變量。
傳感器的頻率響應描述比例因子(KA)相對于頻率的值。在MEMS加速度計中,頻率響應主要有兩個貢獻因素:(1) 其機械結構的響應;(2) 其信號鏈中的濾波響應。等式3提供了一個通用二階模型,其近似描述了MEMS加速度計機械部分對頻率的響應。在該模型中,fO表示諧振頻率,Q表示品質因數(shù)。
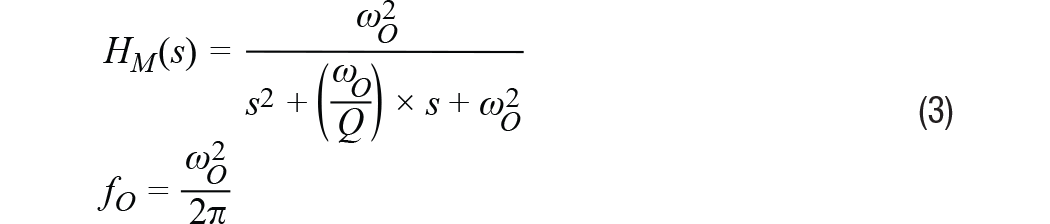
信號鏈的貢獻常常取決于應用所需的濾波。某些MEMS加速度計使用單極點低通濾波器來幫助降低諧振頻率時的響應增益。等式4為此類濾波器相關的頻率響應(HSC)提供了一個通用模型。在該類濾波器模型中,截止頻率(fC)表示輸出信號幅度比輸入信號低√2倍時的頻率。

等式5將機械結構(HM)和信號鏈(HSC)的貢獻進行了合并。
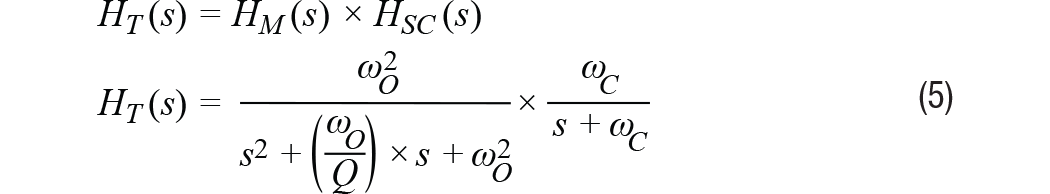
圖3直接應用此模型來預測ADXL356(x軸)的頻率響應。此模型假設標稱諧振頻率為5500 Hz,Q為17,使用截止頻為1500 Hz的單極點低通濾波器。注意,等式5和等式4僅描述了傳感器的響應。此模型未考慮加速度計與其監(jiān)控的平臺的耦合方式。

圖3.ADXL356頻率響應
帶寬與平坦度的關系
在利用單極點低通濾波器(例如等式4所用)建立頻率響應的信號鏈中,其帶寬規(guī)格常常說明了其輸出信號提供輸入信號50%功率時的頻率。對于更復雜的響應,例如等式5和等式3中的三階模型,帶寬規(guī)格常常帶有相應的平坦度規(guī)格。平坦度特性描述比率因子在頻率范圍(帶寬)內的變化。利用圖3和圖5中的ADXL356仿真,1000 Hz時的平坦度約為17%,2000 Hz時的平坦度約為40%。
雖然許多應用由于平坦度(精度)要求而需要限制可以使用的帶寬,但對有些應用來說,這可能不是問題。例如,某些應用可能更注重跟蹤隨時間的相對變化,而不是絕對精度。另一個例子是利用數(shù)字后處理技術來消除用戶最關心的頻率范圍上的紋波。對于此類情況,在給定頻率范圍時,響應的可重復性和穩(wěn)定性常常比響應的平坦度更重要。
測量范圍
MEMS加速度計的測量范圍指標表示傳感器的輸出信號可以跟蹤的最大線性加速度。在超出額定測量范圍的線性加速度水平,傳感器的輸出信號會飽和。這種情況會引起嚴重失真,導致難以(甚至無法)從測量結果提取有用信息。因此,必須確保MEMS加速度計能夠支持峰值加速度水平(參見圖2中的AMAX)。
注意,測量范圍與頻率有一定的關系,因為傳感器的機械響應會引入某種響應增益,增益響應的峰值出現(xiàn)在諧振頻率時。對于ADXL356的仿真響應(參見圖3),增益峰值約為4倍,故測量范圍從±40 g降至±10 g。等式6提供了一種分析方法來預測此值,它以等式5為出發(fā)點:
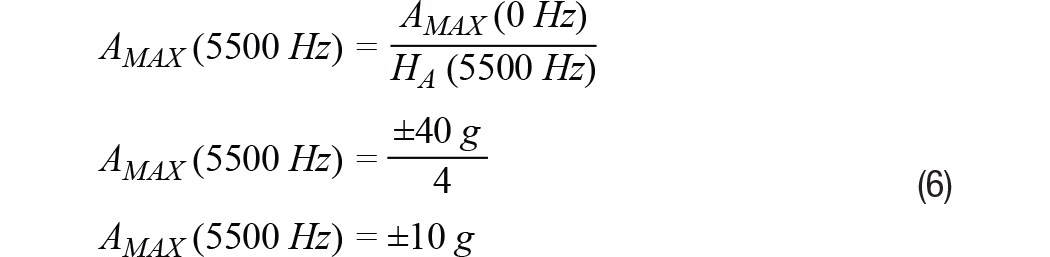
比例因子的大幅變化和測量范圍的降低,是大多數(shù)CBM系統(tǒng)希望將其遭受的最大振動頻率限制在遠低于傳感器諧振頻率水平的兩個原因。
分辨率
儀器分辨率可定義為環(huán)境中引起儀器示數(shù)發(fā)生可檢測變化的最小值。"1在振動檢測節(jié)點中,加速度測量的噪聲會直接影響其檢測振動變化的能力(即"分辨率")。因此,對于那些正在考慮利用MEMS加速度計檢測其機器平臺上微小振動變化的人來說,噪聲行為是一個重要考慮因素。等式7提供了一個用于量化MEMS加速度計噪聲對其分辨微小振動變化能力的影響的簡單關系式。在該模型中,傳感器的輸出信號(yM)等于其噪聲(aN)與其經受的振動(aV)之和。因為噪聲(aN)與振動(aV)沒有相關性,所以傳感器輸出信號的幅度(|yM|)等于噪聲幅度(|aN|)與振動幅度(|aV|)的和方根(RSS)。
那么,需要何種振動水平才能克服測量中的噪聲負擔,在傳感器輸出信號中產生可觀測的響應?根據(jù)噪聲水平量化振動水平有助于以分析方式探究這個問題。等式8通過比率(KVN)確定了這一關系,然后根據(jù)該比率導出了一個預測傳感器輸出變化水平的關系:
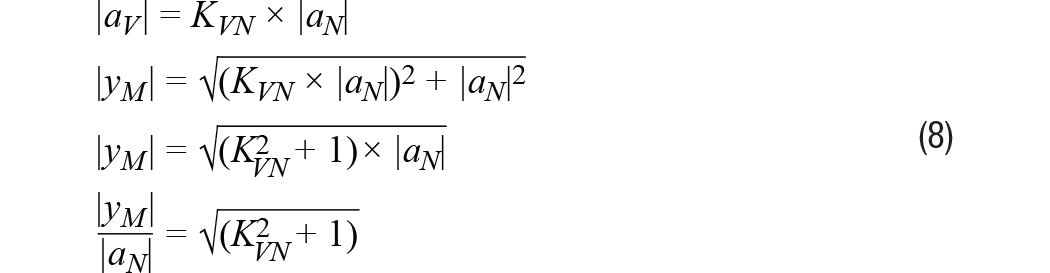
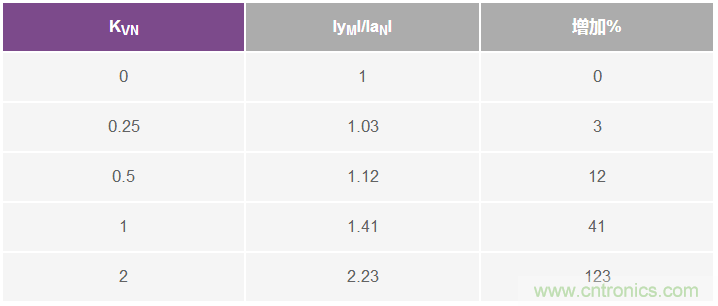
表1提供了此關系的一些數(shù)值例子,以幫助說明傳感器輸出測量結果相對于振動與噪聲幅度之比(KVN)的增加。為簡明起見,本文剩余部分假設傳感器測量的總噪聲決定其分辨率。從表1可知,這對應于KVN為1的情況,即振動幅度等于噪聲幅度。在這種情況下,傳感器的輸出幅度相對于零振動時的輸出幅度會增加42%。注意,為了確定該情況下分辨率的相關定義,每種應用可能需要考慮系統(tǒng)中可觀測到何種水平的增加。
Table 1. Sensors Response to Vibration/Noise
預測傳感器噪聲
圖4顯示了一個采用MEMS加速度計的振動檢測節(jié)點的簡化信號鏈。大多數(shù)情況下,低通濾波器會提供某種抗混疊支持,而數(shù)字處理會提供更明確的頻率響應邊界。一般而言,這些數(shù)字濾波器會努力保護代表實際振動的信號內容,同時將帶外噪聲的影響降至最低。因此,當估計噪聲帶寬時,數(shù)字處理是系統(tǒng)中要考慮的影響最大的部分。此類處理可采用時域技術,例如帶通濾波器,或采用頻譜技術,例如快速傅里葉變換(FFT)。
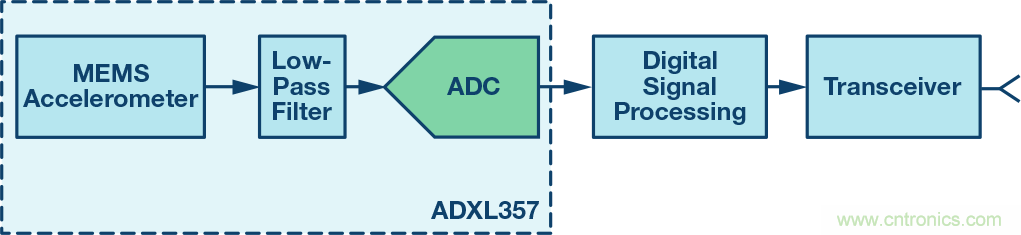
圖4.振動檢測節(jié)點信號鏈
等式9提供了一個用于估計MEMS加速度計測量總噪聲(ANOISE)的關系式,其中使用了噪聲密度(φND)和與信號鏈相關的噪聲帶寬(fNBW)。
利用等式9中的關系,我們可以估計:當對ADXL357(噪聲密度為80 μg/√Hz)使用噪聲帶寬為100 Hz的濾波器時,總噪聲將為0.8 mg (rms)。
用速度衡量振動
某些CBM應用需要用線速度來衡量核心加速度特性(范圍、帶寬、噪聲)。進行這種轉換的一種方法是從圖1所示簡單模型開始,并使用同樣的假設:線性運動、單一頻率和零平均位移。等式10通過圖1中物體瞬時速度(vV)的數(shù)學關系式表述了該模型。此速度的幅度(表示為均方根rms)等于峰值速度除以√2。

等式11對此關系求導,得出圖1中物體瞬時加速度的關系式:
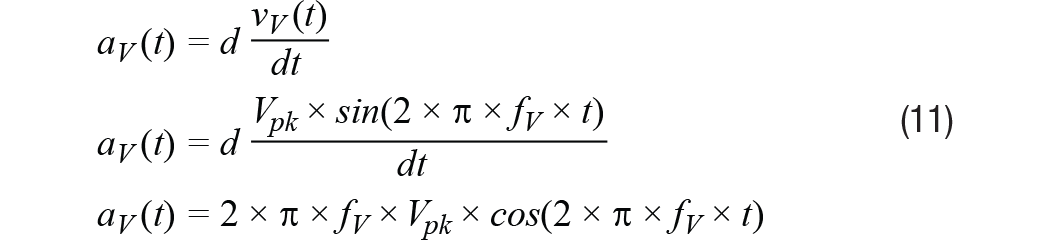
從等式11中加速度模型的峰值出發(fā),等式12導出了加速度幅度(Arms)與速度幅度(Vrms)和振動頻率(fv)的新關系式。

案例研究
現(xiàn)在以ADXL357為例進行研究,將上述內容匯總起來,用線速度表示其范圍(峰值)和1 Hz至1000 Hz振動頻率范圍內的分辨率。圖5提供了對本案例有影響的多個特性的圖形定義,從ADXL357噪聲密度相對于1 Hz至1000 Hz頻率范圍的關系曲線開始。為了簡化討論,本案例研究中的所有計算均假設全部頻率范圍內的噪聲密度為恒定值(φND = 80 μg/√Hz)。圖5中的紅色頻譜曲線表示帶通濾波器的頻譜響應,綠色豎直線表示單一頻率(fV)振動的頻譜響應,其對基于速度估計分辨率和范圍會很有用。

圖5.研究案例的噪聲密度和濾波
此過程的第一步是利用等式9估計四個不同噪聲帶寬(fNBW)產生的噪聲(ANOISE):1 Hz、10 Hz、100 Hz和1000 Hz。表2用兩個不同單位的線速度給出了這些結果:g和mm/s2。g在多數(shù)MEMS加速度計規(guī)格表中相當常見,但振動指標常常不是以此來提供。幸運的是,g和mm/s2的關系已為大家熟知,參見等式13。
表2.傳感器對振動/噪聲的響應
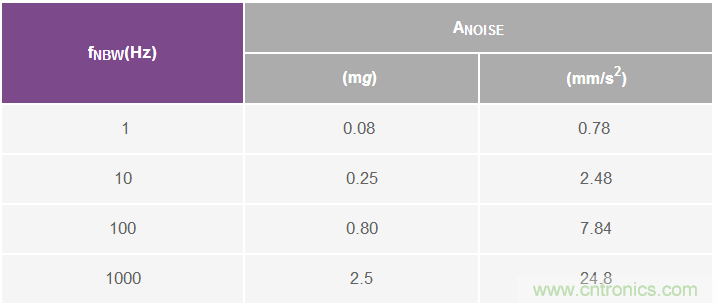
本案例研究的下一步是整理等式12中的關系,以導出一個簡單的公式(參見等式14)來將總噪聲估計(來自表2)轉換為線速度項(VRES、VPEAK)。除了提供此關系的一般形式之外,等式14還提供了一個特定例子,其使用10 Hz的噪聲帶寬(及2.48 mm/s2的加速度噪聲,來自表2)。圖6中的四條虛線表示所有四種噪聲帶寬下相對于振動頻率(fv)的速度分辨率。
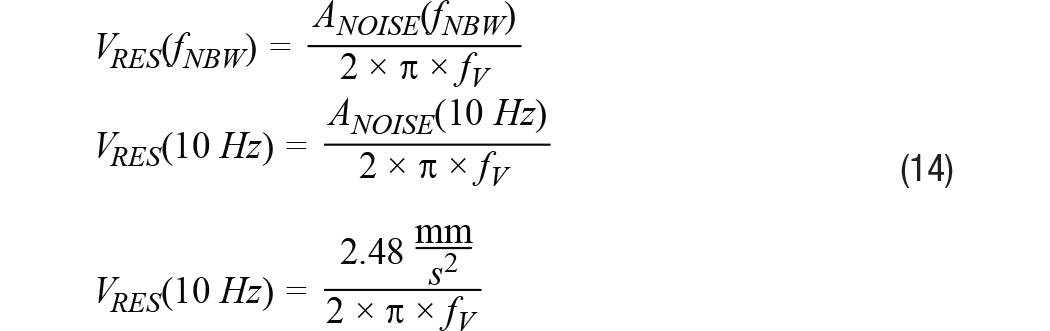
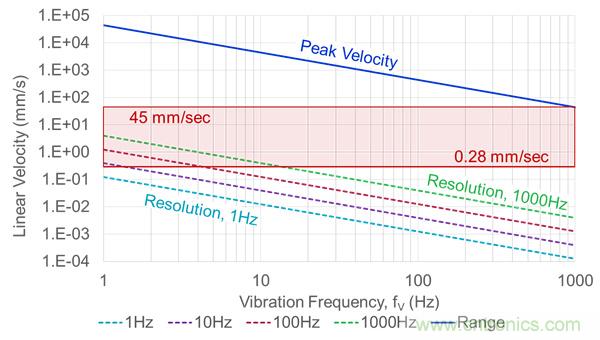
圖6.峰值和分辨率與振動頻率的關系
除了顯示各帶寬對應的分辨率之外,圖6還有一條藍色實線,其表示相對于頻率的峰值振動水平(線速度)。這來自等式15中的關系,其一般形式與等式14相同,但不使用分子中的噪聲,而使用ADXL357支持的最大加速度。注意,分子中的系數(shù)√2會放大此最大加速度以反映均方根水平,假設采用單一頻率振動模型。
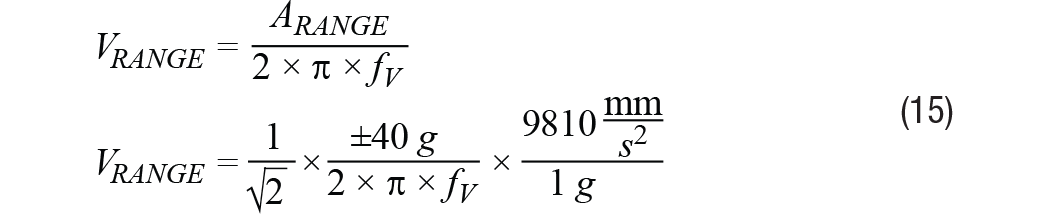
最后,紅框說明如何將此信息應用于系統(tǒng)級要求。此紅框中的最小(0.28 mm/s)和最大(45 mm/s)速度來自關于機器振動的常用工業(yè)標準中的一些分類水平:ISO-10816-1。將關于ADXL357范圍和分辨率曲線的要求放在一起便可快速得出一些簡單的結論,例如:
1.測量范圍的最差情況是在最高頻率時,ADXL357的±40 g范圍似乎能夠測量很大一部分的ISO-10816-1相關振動模式。
2.當用噪聲帶寬為10 Hz的濾波器處理ADXL357的輸出信號時,ADXL357似乎能夠在1.5 Hz至1000 Hz頻率范圍內解析ISO-10816-1中的最低振動水平(0.28 mm/s)。
3.當用噪聲帶寬為1 Hz的濾波器處理ADXL357的輸出信號時,ADXL357似乎能夠在1 Hz至1000 Hz的全部頻率范圍內解析ISO-10816-1中的最低振動水平。
結語
MEMS已是成熟的振動傳感器,在現(xiàn)代工廠CBM系統(tǒng)的技術融合完美風暴中發(fā)揮著重要作用。檢測、連接、存儲、分析和安全領域的新解決方案全都互相融合,為工廠管理者提供完全集成的振動觀測和過程反饋控制系統(tǒng)。雖然很容易迷失在所有此類驚人技術進步所帶來的興奮之中,但人們仍需要了解如何將傳感器測量結果與實際條件和其代表的含義聯(lián)系起來。這些簡單的技術和見解提供了一種將MEMS性能規(guī)格轉換為使用熟悉的單位表示的其對關鍵系統(tǒng)級標準影響的方法,CBM開發(fā)商及其客戶將能從中獲取價值。
參考電路
1. Gerald C. Gill and Paul L. Hexter. “IEEE地球科學電子論文集.” IEEE,第11卷第2期,1973年4月。
推薦閱讀:







